2.1 クーロンの法則
rは点電荷からの位置ベクトル
2.2 重ね合わせの原理
点電荷が1つだけではなく、複数ある場合はどうなるかを考える。この場合は(自分は周りの電荷に影響を及ぼさないとすれば、の話をしているわけだが)、単純に複数の電荷からの寄与を合算すればいい。
これを拡張することで電荷分布・密度が与えられた時も微小な点電荷を積分することで働く力を算出することができる。
2.3 電場
クーロンの法則は点電荷q1が別の点電荷q2が作る電場を感じて力を受けていると考えられる。つまり、
だと考えるときこのEを電場と呼んでみる。
2.4 ガウスの法則
細かい証明は省略するが(手抜きともいう*1)上記のような関係が成り立つ。あ、dsのsは大文字Sの間違い。直すのめんどくさいので・・。Q:閉曲面S内にふくまれる電荷,En:閉曲面Sに垂直なEの成分, dS:微小面積
2.4 電位
A→Bまで単位電荷をもった点電荷を動かす仕事を考えたい。
符号は重力mgを受けながらh上昇させた時に仕事W=mgh(>0)をする(重力方向は下で、かける力は上)ことを考えればマイナスを付けねばならない。(ということをいちいち書くのはサイエンス社の演習書で何やら不思議な記述を見たからなのであるが・・。でも数学の演習書といい、途中で辻褄が合うようにかいてあるので、自分が理解していない何かを行なっているのかもしれないのだが。)
ところでq=1としていたから、
と書いて良かろう。
これは任意の道筋Cについて成り立つ。だから、これは以下のように書き換えることができる。
さて、このような関係式からどうにかEとφのシンプルな関係式を導き出したい。 そのために、x,y,zをそれぞれ微小量だけ増やした時の仕事をかんがえてみる。
まぁこれは良いであろう。(近似式ではあるが、微小量なので・・)
同じ事をEのx成分を用いて表してみる。
(xの変化は微小なのでExはその範囲で同じと考えても差し支えない)
このことから、
とかける。y,z成分についても同様のことは言えるわけで、さてx成分はxの偏微分、・・・となるのは、gradを用いて以下のように表せるのであった。
2.5 静電気・静磁場でのMaxwell方程式(その2)
さて、ベクトルの性質から、rot(grad f)=0 (正確には零ベクトル)*2
なので、
が得られる。
--
*1 あとで証明するかもしれないが、本筋からそれる気がするので別の回に述べる。
*2 ∇×(∇f)=(∇×∇)f=0・f=0
--
参考文献 Feynman Lectures on Physics




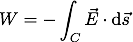






0 件のコメント:
コメントを投稿