ここでは静電場の場合のMaxwell方程式の1つめ∇E=ρ/εを導出したい。そのために手始めにガウスの定理を証明せねばならない。
3.1ガウスの定理
ある閉曲面(体積V,表面積S)から流れだす流体の量を算出したい。
そこで表面の微小面積dSを通る流量を表面全体にわたって積分を実行する。
その表面におけるベクトルEと法線ベクトルnを使うと、流量は
さて、同様の議論を微小の立方体に適用する。頂点は(x,y,z)と各成分にdx,dy,dzを足した8つ。
法線ベクトルがx方向かその逆である、つまりyz平面での流量を算出する。
符号はともかく、それぞれ
E(x) dy dz
E(x+dx) dy dz
とかけよう。ところで、近似的に
E(x+dx)=E(x)+∂E/∂x dx
とかけるから、これらの差は(*レゴブロックの1つだけのピースで形を作る感じ。ピースが無限に小さければ(原子程度)理論上は任意の立体を再現できる。)
(面積分⇔体積積分)
3.2 静電場のMaxwell方程式ガウスの法則から
ところで、Qは連続的な電荷分布を考えれば
ここで先に証明したガウスの定理(定理と法則は別物)から、積分記号の内側を比較すると
つまり、
これと前回示した
の2つを合わせれば静電場に関する基本公式が導きだされたことになる。
3.3 Poisson方程式
ちなみにフランス語でpoissonとは「魚」。魚方程式・・ではなくポアソンという人名だというのはわかっているのだが・・。
それはさておき、前述のdivE=ρ/ε, E=-gradφであることから、以下のことが言える
この∇・∇をΔと書いて、ラプラシアンという。(あ、εの形が違う。まぁいいか。)つまり、
と書き換えられる。この方程式をPoisson方程式と呼ぶ。
--
updated on 24 Fri 2012 (無限小の立方体に関する注釈)






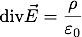



0 件のコメント:
コメントを投稿