4.1 電気双極子
xyz空間でz軸上に距離dだけ離れた電荷2つ(異符号)が置いてある状況を考えてみる。このとき、ポテンシャルは以下のようにかける。
電気双極子というのは、dが小さい場合の一組の電荷をいう。そこで、d→0の極限でのφについて考えてみる。
(z-d/2)^2=z^2+zd+d^2/4
であるが、dは微小量であることを考えれば、一次の項のみをのこして、
(z-d/2)^2=z^2-zd
と近似できる。ここでr^2=x^2+y^2+z^2を導入すればこのことから、
-1/2乗の部分を二項定理で展開することで(一般の二項展開)近似式を更に導きだそう。展開といっても、dの1次までの近似とする。*1
すると、0次の係数: 1、1次の係数: (-1/2)/1=-1/2
よって、
同様に-dの場合も計算され、これらの和から、
(もちろん、d→0での近似ではあるが)
ここで、qdを2つの電荷の双極子モーメントと呼んで、pで表す。
次に、cosθ=z/dを導入すると、θはz軸、原点と点(x,y,z)を結んだ直線、とがなす角であり、
これを動径方向のベクトルrを用いて内積で書き直すと、
となる。これを双極ポテンシャルという。(あ、pもベクトル。p=(0,0,p))
また、rの部分に注意すれば
ともかける。
4.2 コンデンサー
誘電体の話とは切っても切り離せないのがコンデンサーの問題。
高校でお馴染みの公式をいくつか導出できる。
まず、表面積Sの金属板2枚が距離dで隔てられているとする。この電位差をV, 金属板の「面」電荷密度σ、各々の電荷Qとする。
さて、ガウスの法則の方から、双方の電極からの寄与を考慮して、隙間での電場は
ES=Q/ε
つまり
ところで、Vは単位電荷をdだけ移動するときにする仕事であったから、
これを書き換えれば、おなじみの が言える。
さて、誘電体の話を書く準備までできたが、長くなりすぎたので次の記事に移ろうと思う。
--
*1 一般の二項係数はΓ関数で定義される。
Γ(1/2)=√π (∵ガウス積分)
が、今はあまり関係ない。
--
(かなり)参考文献
Feynman Lectures on Physics
(すこし)参考文献
新・演習 電磁気学(サイエンス社)







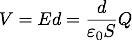


0 件のコメント:
コメントを投稿