7.1 ベクトルポテンシャル
電場の場合
E=-grad φ
とかけた。これは、
rot E=0
だったからであるが、磁場の場合は
div B = 0
である。ところで、div rot Cを計算してみると、2階以上偏微分は基本的には順番によらないので、
div rot C = 0
である。ということは、
div B = div (rot A) = 0
と考えることは可能であろう。すなわち、
B=rot A
この場Aをベクトルポテンシャルと呼ぶ。7.2 電流の作るベクトルポテンシャル
静磁場の基礎方程式
からはじめる。Bを先のAで置き換えると
とかける。外積の性質から、左辺は
c^2∇(∇・A)-(∇・∇)A=c^2∇(∇・A)-ΔA
ここでΔはラプラシアンである。ちなみに、rot grad C = 0であるから、Aにはあるベクトル場φのgradを書きたしても同じ性質を満たす。
つまり、
A'=A+gradφ
このdivをとってみよう。
divA' = div A + div grad φ = div A + Δφ
ここで、先の計算を簡単にするために以下のような条件を付そう。
div A = 0
こうすると、基礎方程式から変形することで
を得る。これは各成分ごとに3つの式があることを意味している。
さて、この形式の方程式は静電場の際にもPoisson方程式として出ている。
電流密度jと電荷密度qが対応すると考えれば、電流密度jからベクトルポテンシャルAを求め、そのrotを取ることでBを得ることができる。
7.3 ビオ・サバールの法則
上記の議論を定式化する
まずx成分を見てみる これを全成分について考えれば、
(Bの添字は見なかったことに・・。) これを、ビオ・サバールの法則という。
さて、あとは誘導を終わらせて最後の形に仕上げる。
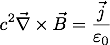




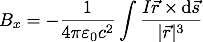
0 件のコメント:
コメントを投稿